多重比较校正方法，并在R中实现。

为什么要进行多重比较校正

当在同一个数据集上进行多次统计检验时，就需要进行多重比较校正。举个简单的例子，A、B两组被试，我们从每个被试身上得出10个指标。如果我们要研究A、B两组被试的某一个指标是否存在显著差异，那么此时我们只做一次统计分析就行；假设这个指标的p值小于0.05，我们会认为这个指标在A、B两组之间存在显著差异，此时，我们犯错的概率（或者称为假阳性率）是5%。假设我们把这10个指标都进行了统计分析，即使每个独立的指标的p值都小于0.05，此时我们犯错的概率不再是5%，至少有一个false positive的概率是1－（0.95）^10=0.4013，也就是说此时我们犯错的概率达到40%多，这在统计学上是不可接受的。因此，需要进行多重比较校正。

因为假设检验是对原假设有利。（对，因为它本质上是一个反证法）。思想：

先预设原假设是成立的
那么看看当前的情况在原假设的条件下是不是极小概率事件，比如发生概率<5%
如果是的话。那原假设就很可疑，迫不得已认为它不成立
不是的话。那原假设就凑活着用吧
如果你多次使用假设检验，还好死不死全都通过了的话！
你的逻辑链条里将出现大量“就凑活着用吧”的命题，当然不靠谱啦！

矫正方法

在多重假设检验中，有不同的控制指标，包括：

Per comparison error rate (PCER, 比较误差率): Type I Error的期望数目比总假设数
Family-wise error rate (FWER): 至少出现1次Type I Error
False discovery rate (FDR, 错误发现率): Type I Error在总拒绝数量中的比率（错误拒绝率）
Positive false discovery rate (pFDR, 阳性错误发现率): 错误发现的比率
在实际应用中，我们一般希望减少Type I Error出现（错误拒绝H0）的可能，因此主要考虑FWER和FDR这两个数据。FWER指标有Bonferroni 校正和Holm’s方法；FDR指标有Benjamin and Hochberg (BH)方法。

基于Bonferroni 法的校正过程

算法

Family-wise error rate ：

$\alpha_{FW} = 1-(1-\alpha_{PC})^c$

c为总检验次数（即P值的个数）; α_PC为每次比较中的错误率（通常为0.05）。所以在3次比较中，α_FW的值为 1-(1-0.05)^3 = 0.143。
有两种方法进行矫正（如下图）：

Approach 1：将原始的p-value和 α_PC /3 = 0.05/3 = 0.017 比较，原始P value小于矫正后的p-value（如0.017）即可认为是显著差异的p-value；
Approach 2：将原始的p-value和总检验次数（如3）相乘，得到矫正后的p-value，如果矫正后的p-value可认为是显著差异的p-value；

如果原始的P值为0.05，检验次数为10000次，那么在Bonferroni 校正中，校正的阈值就等于5%/ 10000 = 0.000005，所有P值超过0.00005的结果都被认为是不可靠的。这样的话假阳性结果在10000次检验中出现的次数为 10000 * 0.000005 =0.5，还不到1次。

优缺点

Bonferroni 校正法可以称作是“最简单粗暴有效”的校正方法，它拒绝了所有的假阳性结果发生的可能性，通过对p值的阈值进行校正来实现消除假阳性结果。但是这也存在问题：Bonferroni 委实太过严格，被校正后的阈值拒绝的不只有假阳性结果，很多阳性结果也会被它拒绝。

R实现

1
2
3

p=c(0.053,0.001,0.045,0.03,0.02,0.01)
p.adjust(p,"bonferroni")
[1] 0.318 0.006 0.270 0.180 0.120 0.060

基于BH法的FDR校正过程

算法

举个例子，我们最开始设定的情况中进行了10000次检验，这次我们设定FDR在一定的范围，如FDR<0.05，如果我们的检验对象为差异表达的基因，那么在10000次检验中假如得到了500个基因，那么这500个基因中的假阳性结果小于 500*5% = 25 个。比较常用的BH发算法如下：

BH 法需要将总计m次检验的结果按由小到大进行排序，k为其中一次检验结果的P值所对应的排名。
找到符合原始阈值α的最大的k值，满足P(k)<=α*k/m，认为排名从1到k的所有检验存在显著差异，并计算对应的q值公式为q = p*(m/k)。
举个例子，如果我们有总共六个结果进行FDR校正：
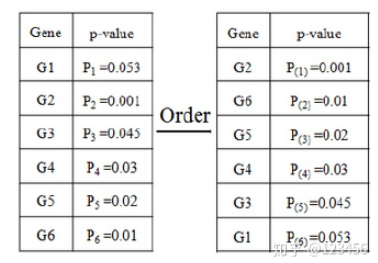
按α=0.05进行计算：
排名第四的 P (4) = 0.03 < 0.05*4/6 = 0.033，符合要求
排名第五的 P (5)= 0.045 > 0.05*5/6 = 0.041，不满足P(k)<=α*k/m，因此在这个列表里排名前四的G2,G6,G5,G4 为具有显著差异的基因。

我们也可以用q值进行FDR校正：

q-value = P * (k/m)
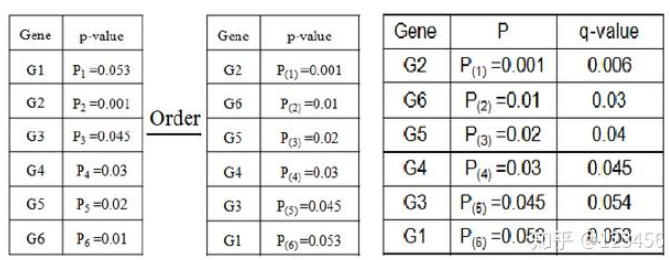
排名第五的G3，其q值大于0.05，故G2,G6,G5,G4 为具有显著差异的基因。

优缺点

相对Bonferroni 来说，FDR温和得多，这种校正方法不追求完全没有假阳性结果，而是将假阳性结果和真阳性的比例控制在一定范围内。

R实现

1
2
3

p=c(0.053,0.001,0.045,0.03,0.02,0.01)
p.adjust(p,"BH")
[1] 0.053 0.006 0.053 0.045 0.040 0.030

引用

谈一谈两种常用的多重比较校正方法
 多重检验，P值校正
 多重假设检验及其生物学应用
 多重假设检验：Bonferroni 和 FDR
how2stats - What is the Bonferroni Correction?
StatQuest - False Discovery Rates, FDR, clearly explained

参考文章如引起任何侵权问题，可以与我联系，谢谢。